Workshop Abstracts
Title: Surfaces with Completely Degenerate Kontsevich-Zorich Spectrum are Completely Periodic
Author(s): David Aulicino/University of Maryland - College Park
We define the rank one locus to be the set of points in the moduli space of surfaces carrying holomorphic Abelian differentials such that the derivative of the period matrix has rank one. There are examples in genus 3 and 4 of surfaces whose Teichmüller disks are contained in the rank one locus. In particular, this implies that if a surface or SL2(
)-invariant measure admits a Kontsevich-Zorich spectrum, then the spectrum is completely degenerate, i.e. λ1 = 1 > λ2 = … = λg = 0. A surface X carrying an Abelian differential ω is completely periodic if every direction that admits a cylinder admits a decomposition of X into cylinders with parallel waist curves. We prove that if a surface has a Teichmüller disk which is contained in the rank one locus, then it is a completely periodic surface.
Title: On concave univalent functions
Author(s): Bappaditya Bhowmik/Indian Institute of Science, S. Ponnusamy (IIT Madras, India); K-J. Wirths (Institute for Analysis and Algebra, TU Braunschweig,Germany)
One of the most important subclasses of the class of normalized analytic univalent functions on the open unit disc D is the class of convex functions. In this talk we will focus on meromorphic analogues of the results known for this class. I.e. we consider functions that map D conformally onto a set whose complement is a bounded convex set. We shall begin with a brief history of Livingston's conjecture which concerns the exact set of variability of the Taylor coefficients for concave functions. Thereafter, we shall discuss some new results concerning the closed convex hull of concave functions and extreme points of it.
Title: Wild singularities of translation surfaces
Author(s): Joshua Bowman/Stony Brook University, Ferran Valdez (Instituto de Matemáticas Unidad Morelia)
Cone-type singularities have played a crucial role in the classical theory of compact translation surfaces. For a non-compact surface, singularities appear as points of the metric completion, and the behavior of the surface near such points can be extremely complicated. We introduce an affine invariant for these singularities in a way that naturally extends the tangent bundle of the surface, and we use this invariant to distinguish among several recently-discovered classes of translation surfaces having the same (infinite) topological type.
Title: On the Growth of the Weil-Petersson Diameter of Moduli Space
Author(s): Will Cavendish/Princeton University, Hugo Parlier/EPFL
The Weil-Petersson metric on Teichmüller space is a negatively curved Kähler metric that relates in interesting ways to hyperbolic geometry in dimensions 2 and 3. Though this metric is incomplete, its completion is a CAT(0) metric space on which the mapping class group acts cocompactly, and the quotient of this completion by the mapping class group is the Deligne-Mumford compactification of moduli space 
. I will give a brief introduction to Weil-Petersson geometry and discuss joint work with Hugo Parlier that studies the growth of diam() as g and n tend to infinity.
Title: Dynamical systems have badly approximable points
Author(s): Jon Chaika/University of Chicago
Let T : [0,1] → [0,1] be a Lebesgue measure preserving map. Then there exists c > 0 such that for Lebesgue almost every point x0 we have 
. This generalizes to higher dimensions.
Title: The crooked plane conjecture
Author(s): Virginie Charette/Université de Sherbrooke, Todd Drumm/Howard University and William Goldman/University of Maryland
The crooked plane conjecture states that any complete flat Lorentzian 3-manifold with free fundamental group arises from a tiling of Minkowski spacetime under the action of a holonomy representation of its fundamental group. We would consequently obtain an explicit topological description of the manifold as a solid handlebody. The problem originates in some work of Margulis in the 1980s, who discovered surprising examples of free groups of isometries acting freely and properly discontinuously on 3d Minkowski spacetime. Drumm introduced crooked planes as a means to describe fundamental domains for these actions, setting the stage for some far-reaching extensions of Margulis' discovery. In joint work with Drumm and Goldman, we proved the crooked plane conjecture for all surfaces of Euler characteristic -1. We will discuss how we proved this using ideal triangulations on these surfaces.
Title: Canonical Thurston obstructions for subhyperbolic semi-rational branched coverings
Author(s): Tao Chen/Graduate Center, CUNY, Yunping Jiang/ Queens College and Graduate Center of CUNY
We prove that the canonical Thurston obstruction for a subhyperbolic semi-rational branched covering exists if the branched covering is not CLH equivalent to a rational map.
Title: Geometric transitions: from hyperbolic cone structures to AdS tachyon structures
Author(s): Jeffrey Danciger/Stanford University
We introduce a geometric transition between two homogeneous three-dimensional geometries: hyperbolic geometry and anti de Sitter (AdS) geometry. Given a path of hyperbolic structures that collapse down onto a hyperbolic plane, we describe a method for constructing a natural continuation of this path into AdS structures. In this talk, we focus on the case of compact three-manifolds with singularities. In particular, when hyperbolic cone manifolds collapse, the AdS manifolds generated on the "other side" of the transition have tachyon singularities, a natural analogue to cone singularities in the AdS setting. Our construction was inspired by ideas of Hodgson and Porti in the case of hyperbolic/spherical transitions.
Title: Tessellations of hyperbolic surfaces
Author(s): Jason DeBlois/Stanford University
The Delaunay tessellation of a hyperbolic surface F determined by a finite set S ⊂ F is a polygonal decomposition of F with vertex set S. Each two-cell is "cyclic'': its interior is isometric to a polygon in 
2 with all vertices on a fixed circle. Such a polygon is "centered'' if it contains the center of its circumcircle. Having non-centered Delaunay two-cells is in some sense undesirable; I will make this precise and describe a way around it.
Title: Average distances and statistical hyerbolicity in Teichmuller space
Author(s): Spencer Dowdall/University of Chicago
The Teichmuller space of a closed surface exhibits many aspects of negative curvature but fails to be hyperbolic in any global sense. In this talk I will discuss the "statistical hyperbolicity" of Teichmuller space as reflected by the average distance between points on a sphere of radius R. I will illustrate how distances on metric spheres behave in the presence of negative vs nonnegative curvature. Although these competing phenomena both influence distances in Teichmuller space, we will see that the average distance is dominated by the negative curvature. Joint work with Moon Duchin and Howard Masur.
Title: Decomposing diffeomorphisms of the sphere
Author(s): Alastair Fletcher/University of Warwick, Vlad Markovic/University of Warwick
A central problem in the area of quasiconformal and bi-Lipschitz homeomorphisms is whether such homeomorphisms of the sphere Sn can be decomposed into homeomorphisms of small conformal or isometric distortion, respectively. Apart from some special cases, little is known. We will discuss the following related result: a C1-diffeomorphism of the sphere Sn can be written as a composition of bi-Lipschitz homeomorphisms with isometric distortion arbitrarily close to 1.
Title: Harmonic Maps into Conic Surfaces With Cone Angles Less Than 2π
Author(s): Jesse Gell-Redman/Stanford University
We discuss the harmonic map problem when the spaces involved are punctured Riemann surfaces. When the target has a conformal metric with cone angles less than π, there is a unique energy minimizing map in every degree one homotopy class. We discuss possible applications to Teichmüller theory.
Title: Random Triangulated Riemann Surfaces
Authors(s): James Gill/University of Washington, Steffen Rohde/University of Washington
We show that the (random) Riemann surfaces of the Angel-Schramm Uniform Infinite Planar Triangulation and of Sheffield’s infinite necklace construction are both parabolic. In other words, Brownian motion on these surfaces is recurrent. We obtain this result as a corollary to a more general theorem on subsequential distributional limits of random unbiased disc triangulations, following work of Benjamini and Schramm.
Asymptoticity of grafting and Teichmüller rays
Author(s): Subhojoy Gupta/Yale University
We shall discuss a result showing that any grafting ray in Teichmüller space is (strongly) asymptotic to a Teichmüller geodesic ray. Our method involves constructing quasiconformal maps between the underlying Thurston metric of a complex projective surface on one hand, and the singular flat metric induced by a holomorphic quadratic differential on the other. One corollary is that the projection of a generic grafting ray to moduli space is dense.
Title: The extrinsic geometry of the handlebody group
Author(s): Sebastian Hensel/Max-Planck Institute for Mathematics Bonn, Ursula Hamenstädt
A handlebody V is a compact 3-manifold bounded by a genus g surface S. The handlebody group Map(V) is the subgroup of the mapping class group Map(S) of S defined by those elements extending to homeomorphisms of V. We study the geometry of Map(V) as a subgroup of Map(S). In particular, we show that it is undistorted for genus g ≤ 2, and distorted for all higher genera.
Title: Small pseudo-Anosov maps and short loops in automata
Authors: Eriko Hironaka/Florida State University
We find explicit train tracks describing the dynamics of a family of orientable pseudo-Anosov mapping classes with conjectural minimal dilatation as a function of genus. We extend this example to give a general description of train track maps for linearly convergent sequences on a fibered face
Title: Minimal surfaces in hyperbolic three-manifolds
Author(s): Zheng Huang, City University of New York, Marcello Lucia/City University of New York
We will discuss several problems involving (incompressible) minimal surfaces in hyperbolic three-manifolds.
Title: Hyperbolization of Metric Spaces
Author(s): Zair Ibragimov/California State University at Fullerton
M. Bonk, J. Heinonen and P. Koskela proved that the quasihyperbolic metric hyperbolizes (in the sense of Gromov) uniform metric spaces. In this talk we discuss a new metric that hyperbolizes all locally compact noncomplete metric spaces. The metric is generic in the sense that (1) it can be defined on any metric space; (2) it preserves the quasiconformal geometry of the space; (3) it generalizes the j-metric, the hyperbolic cone metric and the hyperbolic metric of hyperspaces; (4) it is quasiisometric to the quasihyperbolic metric of uniform metric spaces. In particular, the Gromov hyperbolicity of these metrics also follows from that of our metric.
Title: On the Connectedness of the Branch Locus of the Moduli Mpace of Riemann Surfaces
Author(s): Milagros Izquierdo/Linkoping University, Antonio F. Costa/UNED, Madrid (Spain)
The branch locus of the moduli space of Riemann Surfaces of genus g ≥ 2 is disconnected for all but genera three, four, seven, thirteen and seventeen. But the branch locus becomes connected if one allows the use of symmetries, i.e. anticonformal involutions.
Title: Maximally stretched laminations on hyperbolic maniolds and applications
Author(s): Fanny Kassel/University of Chicago, François Guéritaud (Université Lille 1)
Together with F. Guéritaud, we extend work of Thurston by proving that for any convex cocompact hyperbolic manifold M and any pair (g,h) of distinct hyperbolic metrics on M with common critical exponent, there is a geodesic lamination on M that is maximally stretched by all Lipschitz maps homotopic to the identity whose Lipschitz constant is minimal (for the metrics g and h); in particular, this minimal Lipschitz constant is the supremum of ratios of length of closed geodesics on M. We generalize this result in the setting of equivariant maps in hyperbolic spaces. This applies to the deformation theory of 3-dimensional anti-de Sitter manifolds and Riemannian holomorphic manifolds.
Title: Geometrically infinite surfaces with discrete length spectra
Author(s): Youngju Kim/Korea Institute for Advanced study, Ara Basmajian/ Hunter College, CUNY
It is well-known that the length spectrum of a geometrically finite hyperbolic manifold is discrete. We show that geometrically infinite surfaces admit both an infinite dimensional family of quasiconformally distinct hyperbolic structures having a discrete length spectrum, and an infinite dimensional family of quasiconformally distinct structures with a nondiscrete spectrum. This is a joint work with Prof. Ara Basmajian.
Title: Right-angled Artin groups and mapping class groups
Author(s): Thomas Koberda/Harvard University
I will discuss subgroups of the mapping class group generated by sufficiently large powers of mapping classes. When these mapping classes are Dehn twists or pseudo-Anosovs supported on subsurfaces, we obtain a right-angled Artin group. When the mapping classes are general, we can naturally embed the resulting group in a right-angled Artin group.
Title: Representation theory and harmonic maps
Author(s): Evelyn Lamb/Rice University
Let M be a Riemann surface of genus g ≥ 2 with fundamental group π. Representations from π to PSL(2,) occur in 4g-3 components indexed by Euler class. There is one component for each e such that |e| ≤ 2g-2. This talk is about using harmonic maps to study representations occurring in the non-maximal components of Hom(PSL(2,). This approach is analogous to Wolf's parametrization of Teichmüller space by harmonic maps.
Title: Local and Global Topology of Group-Valued Quiver Representations
Author(s): Sean Lawton/University of Texas-Pan American, Carlos Florentino/Instituto Superior Tecnico
Let G be a complex reductive Lie group. Denote the moduli space of group-valued representations of a quiver Q by M(Q,G). For various general families of G and Q, we will discuss recent results concerning the local and global topology of M(Q,G)
Title: Dynamics on the PSL(2, C)-character variety of a twisted I-bundle
Author(s): Michelle Lee/University of Michigan
Let M be a twisted interval bundle over a nonorientable hyperbolizable surface. Let χ(M) be the PSL(2,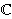 
)-character variety of π1(M). We will discuss the dynamics of the action of Out(π1(M)) on χ(M) and in particular find an open set on which the action is properly discontinuous that is strictly larger than the interior of the deformation space of marked hyperbolic manifolds homotopy equivalent to M. Further, we will identify which discrete and faithful representations can lie in a domain of discontinuity for this action.
Title: Spacefilling curves and phases of the Loewner equation
Author(s): Joan Lind/University of Tennessee, Steffen Rohde / University of Washington
The Loewner differential equation provides a way to generate families of growing sets in the upper halfplane called hulls. This equation has received significant attention since the introduction of Schramm-Loewner Evolution (SLE) by Oded Schramm. One question of interest is how deterministic hulls compare to SLE hulls. We show that there are two deterministic phase transitions, analogous to the two phase transitions for SLE. Additionally, we show that there are natural deterministic hulls with geometry similar to that of SLE.
Title: A Jorgensen-Thurston theorem for homomorphisms
Author(s): Yi Liu/UC Berkeley
In this talk, we describe the structure of homomorphisms from a finitely generated group G to torsion-free Kleinian groups of uniformly bounded covolume. This is an analogy of the Jorgensen-Thurston theorem to homomorphisms.
Title: Minimal Lagrangian Surfaces in CH2 and Represenations into SU(2,1)
Author(s): John Loftin/Rutgers Newark, Ian McIntosh/University of York
We construct minimal Lagrangian surfaces in CH2 which are invariant under a natural SU(2,1) action of a surface group. The technique is to solve an integrability equation on a compact Riemann surface Σ equipped with a cubic differential. This produces a minimal Lagrangian surface invariant under an SU(2,1) action of π1Σ. This story is an analog of Uhlenbeck's theory of minimal surfaces in quasi-Fuchsian hyperbolic 3-folds.
Immersed surfaces in the modular orbifold
Author(s): Joel Louwsma/California Institute of Technology, Danny Calegari/California Institute of Technology
A hyperbolic conjugacy class in the modular group PSL(2,Z) corresponds to a closed geodesic in the modular orbifold. Some of these geodesics virtually bound immersed surfaces, and some do not; the distinction is related to the polyhedral structure in the unit ball of the stable commutator length norm. We prove the following stability theorem: for every hyperbolic element of the modular group, the product of this element with a sufficiently large power of a parabolic element is represented by a geodesic that virtually bounds an immersed surface. This is joint work with Danny Calegari.
Title: Volume and fillings of high-dimensional hyperbolic manifolds
Author(s): Jason Manning/University at Buffalo, Koji Fujiwara/Tohoku University
Given a finite volume hyperbolic manifold (of any dimension) with torus cusps, nonpositively curved "Dehn fillings" of the manifold can be defined. These pseudomanifolds have simplicial volume which can be estimated from above in terms of the volume of the original manifold. I'll outline the proof, and pose some questions about refining these bounds, and about whether or not the proof can be recast in deformation theoretic terms.
Title: On Cusp Finiteness for higher dimensional Kleinian groups with critical exponent less than one
Author(s): Dustin Mayeda/University of California, Davis
In the late 1970's Sullivan proved that a finitely generated three dimensional Kleinian group has only finitely many cusps. The straight forward generalization of Sullivan's theorem to higher dimensions does not hold as shown by examples of Kapovich and Potyagailo. I will discuss a condition on higher dimensional Kleinian groups which implies that they have finitely many cusps.
Lipschitz and bi-Lipschitz Maps on Carnot Groups
Author(s): William Meyerson/UCLA
Suppose A is an open subset of a Carnot group G and H is another Carnot group. We show that a Lipschitz function from A to H whose image has positive Hausdorff measure in the appropriate dimension is biLipschitz on a subset of A of positive Hausdorff measure. We then construct Lipschitz maps from open sets in Carnot groups to Euclidean space that do not decrease dimension. Finally, we discuss two counterexamples to explain why Carnot group structure is necessary for these results.
Title: Teichmuller rays and Gardiner-Masur boundary of Teichmueller space
Author(s): Hideki Miyachi /Department of Mathematics, Osaka University
I will observe that any Teichmüller rays converges in the Gardiner-Masur compactification. Therefore, we have a mapping from the space of projective measured foliations to the GM-boundary by assigning the limits of associated Teichmüller rays. I will also discuss properties of this mapping.
Title: Backward iteration in the unit ball
Author(s): Olena Ostapyuk/Kansas State University
I will consider analytic self-map f of the unit ball in N. Many facts were established about such maps in the 1-dimensional case (i.e. for self-maps of the unit disk), and I will generalize some of them in higher dimension. In the case when f is hyperbolic or elliptic, it will be shown that backward-iteration sequences with bounded hyperbolic step will converge to a point on the boundary. These points will be called boundary repelling fixed points (BRFPs) and will possess several nice properties. In particular, in the case when such points are isolated from from other BRFPs, they will be completely characterized as limits of backward iteration sequences. Then I will present some important examples and describe problems that arise in the parabolic case.
Title: New non-arithmetic lattices in SU(2,1)
Author(s): Julien Paupert/University of Fribourg, Martin Deraux /Grenoble, John Parker/Durham
The first examples of non-arithmetic complex hyperbolic lattices were constructed by Mostow in 1980. These examples are generalized triangle groups generated by complex reflections of orders 3, 4 or 5. We will see how to generalize Mostow's construction to produce new non-arithmetic lattices in SU(2,1).
The role of hyperbolic geometry in the theory of iteration of self-maps of the disk and the ball
Author(s): Pietro Poggi-Corradini/Kansas State University
We will review the crucial role played by the hyperbolic geometry of the unit disk in the complex plane and the unit ball in several complex variables to study the dynamics of analytic self-maps. We will conclude with a series of open problems and also a description of recent results obtained by my student Olena Ostapyuk.
Title: Burkholder integrals, Morrey's problem and quasiconformal mappings
Author(s): Istvan Prause/University of Helsinki, Kari Astala, Tadeusz Iwaniec, Eero Saksman
Inspired by Morrey's problem (on rank-one convex functionals) and the Burkholder integrals (of his martingale theory) we find the strongest possible Lp-estimates for the Beltrami equation. Roughly put, the Burkholder integrals are quasiconcave with respect to quasiconformal deformations. This is joint work with Kari Astala, Tadeusz Iwaniec and Eero Saksman.
Title: Ending laminations and the Noebeling curve
Author(s): Piotr Przytycki/Institute of Mathematics of the Polish Academy of Sciences, Sebastian Hensel/Bonn University
We prove that the ending lamination space of the five-punctured sphere is homeomorphic to the Nöbeling curve.
Title: Quantum Teichmuller theory and conformal field theory
Author(s): Julien Roger/Rutgers University
The aim of this talk is to describe the construction of the quantum Teichmüller space, emphasizing its relationship with hyperbolic geometry and the Weil-Petersson geometry of Teichmüller space, and then to analyze its relationship with conformal field theory. I will also discuss one of the motivations for this work, which is the construction of a family of representations of the mapping class groups, giving rise to a so-called modular functor.
Title: Circle homeomorphisms and shears
Author(s): Dragomir Saric/CUNY Graduate Center and Queens College
A parametrization of the space of homeomorphisms of the unit circle and of the space of quasisymmetric maps (fixing three points) in terms of shears for Farey tesselation of the hyperbolic plane is given. We discuss some applications to Teichmuller theory.
A fiber structure of the Teichmuller space of a bordered surface
Author(s): Eric Schippers/University of Manitoba, David Radnell/American University of Sharjah, United Arab Emirates
The main result of this talk is that the Teichmuller space of a surface bordered by a finite number of boundary curves homeomorphic to the circle is a fiber space. The base space is the Teichmuller space of the punctured surface obtained by sewing on copies of the punctured disc. The fibers are a set of non-overlapping mappings into the punctured surface, modulo a properly discontinuous group action.
The results are motivated a correspondence between a moduli space in conformal field theory and the Teichmuller space of a bordered surface. Joint work with David Radnell.
Infinite covers, Veech groups and recurrence
Author(s): Martin Schmoll/Clemson University, Chris Johnson/Clemson University
We report ongoing research centered about infinite translation covers of a given translation surface. Our main focus are covers with lattice Veech groups and properties of direction flows on the covers in relation to the flow in the same direction on the base surface. We are particularly interested in recurrent directions and will speak about techniques how to find these on infinite covers.
Title: Character Varieties of surfaces as completely integrable systems
Author(s): Adam Sikora/SUNY Buffalo
It is known that the trace functions of a maximal set of disjoint simple closed curves on a closed surface make its SU(2)-character variety into an (almost) completely integrable dynamical system. We prove an analogous statement for all rank 2 Lie groups. We will discuss the possible generalizations of this result to higher ranks and its applications to quantization of character varieties
Title: Geometric curvature energies: smoothing, self-avoidance and compactness effects
Author(s): Pawel Strzelecki/Institute of Mathematics, University of Warsaw
I shall speak on regularizing, compactness and self-avoidance effects caused by the finiteness of certain energies, defined as multiple integrals w.r.t. Hausdorff measure. Examples of these energies can be regarded as analogues of total curvatures for objects with low smoothness; they include variants of Menger curvature for high-dimensional objects (closed Lipschitz submanifolds and more general surfaces in arbitrary dimension and codimension). We obtain geometric analogues of Sobolev-Morrey imbedding theorems with optimal exponents, and compactness results.
The talk is based on joint projects with H. von der Mosel (RWTH Aachen) and S. Kolasinski and M. Szumanska (Warsaw).
Title: Partial holomorphic semi-conjugacies between rational functions
Author(s): Vladlen Timorin/University - Higher School of Economics
I will state a general result on the existence of partially defined semiconjugacies between rational functions acting on the Riemann sphere. The semiconjugacies are defined on the complements to at most one-dimensional sets. They are holomorphic in a certain sense. The key ingredient in the construction is the uniform convergence of Thurston's algorithm.
Title: Two conjectures of Astala on distortion under planar quasiconformal mappings and related removability problems
Author(s): Ignacio Uriarte-Tuero/ Michigan State University, Michael T. Lacey/GATech, Istvan Prause/University of Helsinki, Xavier Tolsa/Autonomous University of Barcelona - ICREA, Eric T. Sawyer/McMaster University
In his celebrated paper on area distortion under planar quasiconformal mappings (Acta 1994), Astala proved that if E is a compact set of Hausdorff dimension d and f is K-quasiconformal, then fE has Hausdorff dimension at most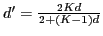 
, and that this result is sharp. He conjectured (Question 4.4) that if the Hausdorff measure 
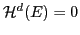, then 
.
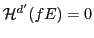UT showed that Astala's conjecture is sharp in the class of all Hausdorff gauge functions (IMRN, 2008).
Lacey, Sawyer and UT jointly proved completely Astala's conjecture in all dimensions (Acta, 2010). The proof uses Astala's 1994 approach, geometric measure theory, and new weighted norm inequalities for Calderón-Zygmund singular integral operators which cannot be deduced from the classical Muckenhoupt Ap theory.
These results are related to removability problems for various classes of quasiregular maps. I will mention sharp removability results for bounded K-quasiregular maps (i.e. the quasiconformal analogue of the classical Painleve problem) recently obtained jointly by Tolsa and UT.
I will further mention recent results related to another conjecture of Astala on Hausdorff dimension of quasicircles obtained jointly by Prause, Tolsa and UT.Title: Asymptotic behavior for pseudo-Anosov mapping classes
Author(s): Aaron Valdivia/Florida State University
The problem of determining minimal dilatations of pseudo-Anosov mapping classes was introduced by Penner who proved that the logarithm of the minimal dilatations on closed surfaces behaved like 
where χg,n is the Euler characteristic of a genus g surface with n punctures. These results have been expanded to asymptotic behavior of minimal dilatations of punctured spheres by Hironaka, Kin, and Tsai and genus 1 surfaces by Tsai. For fixed genus g ≥ 2 Tsai found that the minimal dilatations behaved like 
and asked the question: If we define a plane where the integer points (n,g) are assigned the minimal dilatation for the surface Sg,n what is the asymptotic behavior on other rays? In this talk we will see that the logarithm of the minimal dilatation behaves like for each rational ray emanating from the origin in the gn-plane.
Title: Extremal Annuli On The Sphere
Author(s): Zhe Wang/Graduate Center of the City University of New York, Frederick Gardiner/Graduate Center of CUNY and Brooklyn College
We show how to express the extremal properties of the Teichmuller and Mori annuli in terms of the spherical metric. We also discuss the minimum Dirichlet principle, the minimal axis theorem and show how the extremal annuli appear as minimal axes for pairs of annuli on the four times punctured Riemann sphere and how they are special cases of pairs of annuli of Teichmuller and Mori type.
Title: A Deformation of Penner's Coordinate of the Decorated Teichmüller Space
Author(s): Tian Yang/Rutgers University
We find a one-parameter family of coordinates 
which is a deformation of Penner's coordinate of the decorated Teichmüller space of an ideally triangulated punctured surface (S,T) of negative Euler characteristic. If h≥ 0, the decorated Teichmüller space in the Ψh coordinate becomes an explicit convex polytope P(T) independent of h; and if h < 0, the decorated Teichmüller space becomes an explicit bounded convex polytope Ph(T) so that Ph(T) ⊂ Ph′(T) if h < h′. As a consequence, Bowditch-Epstein and Penner's cell decomposition of the decorated Teichmüller space is reproduced.
Title: Chern-Simons theory and hyperbolic volume
Author(s): Christian Zickert, University of California, Berkeley, Stavros Garoufalidis/Georgia Tech, Dylan Thurston/Columbia
We give a simplicial formula for the Chern-Simons invariant of a flat SL(n,C)-connection (with unipotent holonomy near the boundary) on a compact 3-manifold. Concrete computations reveal the striking new phenomenon that the imaginary part is often (conjecturally always) an integral linear combination of volumes of hyperbolic manifolds.