Abstracts

The structure of high distance Heegaard splittings, Jesse Johnson (Oklahoma State University)

The notion of distance for a Heegaard splitting of a three-dimensional manifold M, introduced by John Hempel, has proved to be a very powerful tool for understanding the geometry and topology of M. I will describe how distance, and a slight generalization known as subsurface projection distance, can be used to explore the connection between geometry and topology at the center of the modern theory hyperbolic three-manifolds.

In particular, Schalremann-Tomova showed that if a Heegaard splitting for M has high distance then it will be the only irreducible Heegaard splitting of M with genus less than a certain bound. I will explain this result in terms of both a geometric proof and a topological proof. Then, using the notion of subsurface distance, I will describe a construction of a manifold with multiple distinct low-distance Heegaard splittings of the same (small) genus, and a manifold with both a high distance, low-genus Heegaard splitting and a distinct, irreducible high-genus, low-distance Heegaard splitting.

Distance and the Cabling Conjecture, Maggy Tomova (University of Iowa)

I will present our recent results that show that any knot with a bridge surface of distance at least three satisfies the Cabling Conjecture. We also have a description for all knots with a bridge surface of distance two. This, together with already known results about knots with bridge surface of distance one, describes all potential counterexamples to the Cabling Conjecture.

Minimal Triangulations of 3-manifolds, William Jaco (Oklahoma State University)

We define the complexity of a compact 3-manifold M to be the minimal number of tetrahedra needed to triangulate M. We will discuss results on finding the complexities of several infinite families of 3-manifolds.

Rank and genus of 3-manifolds, Tao Li (Boston College)

We construct a counterexample to the Rank versus Genus Conjecture, i.e. a closed orientable hyperbolic 3-manifold with rank of its fundamental group smaller than its Heegaard genus. Moreover, we show that the discrepancy between rank and Heegaard genus can be arbitrarily large for hyperbolic 3-manifolds.

The virtual Haken conjecture, Ian Agol (University of California, Berkeley)

We'll describe the proof of Waldhausen's conjecture that aspherical closed 3-manifolds have a finite-sheeted cover which is Haken. The proof reduces to the proof of a conjecture of Dani Wise about cubulated hyperbolic groups being "virtually special" and results of Kahn-Markovic on surface groups in closed hyperbolic 3-manifolds.

Curves in the Masur domain, Saul Schleimer (University of Warwick)

Suppose V is a handlebody with boundary S. The Masur domain M(V) in PML(S) is the maximal open subset where the mapping class group of V acts properly discontinuously. We show if α is a curve in S with distance at least three from the disk set D(V) then α lies in the Masur domain. This answers a question asked independently by Feng Luo and Juan Souto.

Diameter and Homology of Hyperbolic 3-Manifolds, Peter Shalen (University of Illinois, Chicago)

The Mostow rigidity theorem implies that the topological type of a closed, orientable hyperbolic n-manifold M determines M up to isometry. Hence any quantitative geometric invariant of a hyperbolic 3-manifold is in principle a topological invariant. This raises the question of how these geometrically defined invariants compare with more classical topological invariants. For example, if we define the covering radius of M at a point p to be cov_p M = max_{x ∈ M} dist (p,x), a standard elementary argument shows that rank π₁(M) ≤ B exp(2min_{p ∈ M} cov_p M) for some universal constant B. (The rank of π₁ (M) is defined to be its minimal number of generators.) This in particular gives a bound for diam M = max_{p ∈ M} cov_pM in terms of rank(π₁(M)).

The best version of the elementary argument that I know gives a value of about 1000 for B. Using fancy methods, I have shown that if one asks for a bound only on the dimension of H₁(M; Z₂) rather than on rank π₁(M), one can obtain a much better constant. This result is in the course of being written up, but I believe I can now show that

where

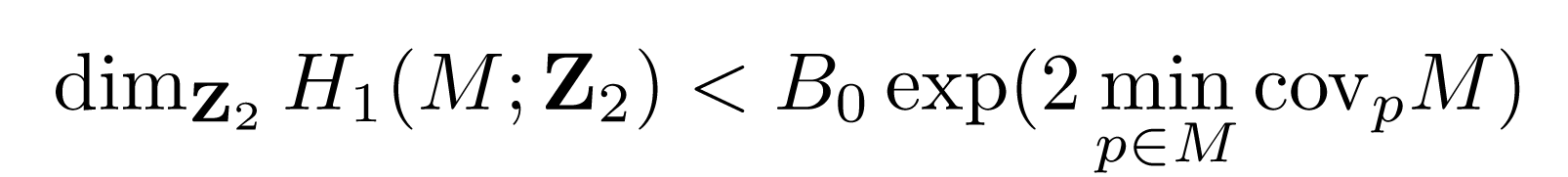
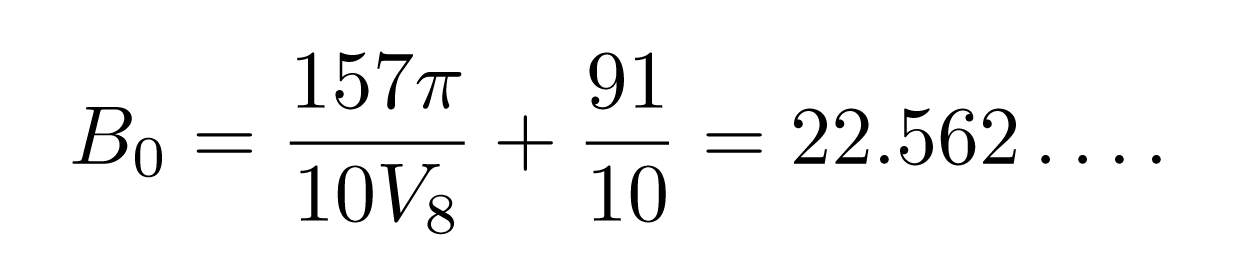
Here V₈ = 3.66386. . .  denotes the volume of a regular ideal octahedron in H³.

The proof, which I will sketch in my talk, relies on earlier work by Culler and myself, and work due to Agol, Storm and W. Thurston. The new ingredients are in large part topological.

Left-orderability of 3-manifold groups, Cameron Gordon (University of Texas, Austin)

We will discuss evidence for the conjecture that a prime rational homology 3-sphere is an L-space if and only if its fundamental group is not left-orderable. This is joint work with Steve Boyer and Liam Watson.